Consideriamo due rette $a$ e $b$ tagliate da una retta trasversale $c$ (“trasversale” indica che $c$ interseca sia $a$ che $b$). Come si può vedere in figura, in entrambi i punti di intersezione di $c$ con le altre due rette vengono a formarsi naturalmente 4 angoli.
Definizione
Facendo riferimento all'immagine precedente diamo le seguenti definizioni:
- gli angoli delle coppie $ (\gamma, \varepsilon), (\zeta, \delta)$ vengono detti alterni interni;
- gli angoli delle coppie $ (\alpha, \eta), (\beta, \theta)$ vengono detti alterni esterni;
- gli angoli delle coppie $ (\gamma, \zeta), (\delta, \varepsilon) $ vengono detti coniugati interni;
- gli angoli delle coppie $ (\beta, \eta), (\alpha, \theta) $ vengono detti coniugati esterni;
- gli angoli delle coppie $ (\alpha, \varepsilon), (\beta, \zeta), (\gamma, \eta), (\delta, \theta)$ vengono detti corrispondenti.
Sappiamo che gli angoli opposti al vertice sono congruenti (come ad esempio $\alpha$ e $\gamma $) ma in generale le coppie di angoli prese in considerazione nella definizione precedente non hanno particolari proprietà. Ma cosa succede quando le rette $a$ e $b$ sono parallele?
TEOREMA: Se due rette parallele parallele $a$ e $b$ vengono tagliate da una trasversale $c$, allora:
- gli angoli alterni (interni o esterni) sono congruenti;
- gli angoli coniugati (interni o esterni) sono supplementari;
- gli angoli corrispondenti sono congruenti.
Nell’immagine che segue, abbiamo quindi le relazioni:
- $\gamma = \varepsilon, \quad \delta = \zeta, \quad \beta = \theta, \quad \alpha = \eta$;
- $\delta + \varepsilon = \gamma + \zeta = \alpha + \theta = \beta + \eta = $ angolo piatto;
- $\alpha = \varepsilon, \quad \beta = \zeta, \quad \gamma = \eta, \quad \delta = \theta$.
In particolare, possiamo riassumere le prima e l’ultima affermazione in questo modo:
##KATEX##\begin{aligned}\alpha & =\gamma = \varepsilon = \eta ; \\\beta & = \delta = \zeta = \theta.\end{aligned}##KATEX##
In realtà, vale anche una sorta di “inverso” del teorema precedente: ovvero, se anche solo due angoli alterni (interni o esterni) o corrispondenti sono congruenti, o se due angoli coniugati sono supplementari, allora le rette tagliate dalla trasversale sono automaticamente parallele. Riassumiamo questa situazione nel seguente:
CRITERIO DEL PARALLELISMO: Condizione necessaria e sufficiente affinché due rette siano parallele è che esse formino con una trasversale una coppia di angoli alterni (interni o esterni) congruenti, oppure due angoli corrispondenti congruenti, oppure due angoli coniugati supplementari.
Citiamo ora un teorema particolarmente interessante che riguarda le rette parallele, che permette di definire senza ambiguità il concetto di distanza tra due rette parallele:
TEOREMA: Segmenti paralleli compresi fra rette parallele sono congruenti fra loro. In particolare, tutti i punti di una retta sono equidistanti dall’altra.
Se tutti i segmenti paralleli sono congruenti tra loro, in particolare, tutti i segmenti perpendicolari sono congruenti. Di conseguenza la distanza di tutti i punti di una retta dall’altra è sempre la stessa. Questa distanza, quindi, può essere considerata come la distanza tra le due rette.
Il teorema di Talete e alcune sue conseguenze
Consideriamo un fascio improprio di rette (cioè, un insieme di rette parallele tra loro) e due trasversali del fascio.
TEOREMA: Un fascio di rette parallele determina sopra due trasversali due insiemi di segmenti direttamente proporzionali. Facendo riferimento al disegno qui sotto, abbiamo, ad esempio: $$\overline{AB} : \overline{AC} = \overline{A_1 B_1} : \overline{A_1 C_1}; \quad \overline{BC} : \overline{CD} = \overline{B_1 C_1} : \overline{C_1 D_1}; \quad \overline{AB} : \overline{CD} = \overline{A_1 B_1} : \overline{C_1 D_1}.$$ In particolare, abbiamo che a coppie di segmenti congruenti su una trasversale corrispondono coppie di segmenti congruenti sull’altra.
Tra le conseguenze di questo teorema, ricordiamo alcune applicazioni ai triangoli.
TEOREMA: Condizione necessaria e sufficiente affinché una retta divida in parti proporzionali due lati di un triangolo (o i suoi prolungamenti) è che sia parallela al lato rimanente.
In particolare, il segmento congiungente i punti medi di due lati di un triangolo è parallelo al terzo lato, e congruente alla sua metà.
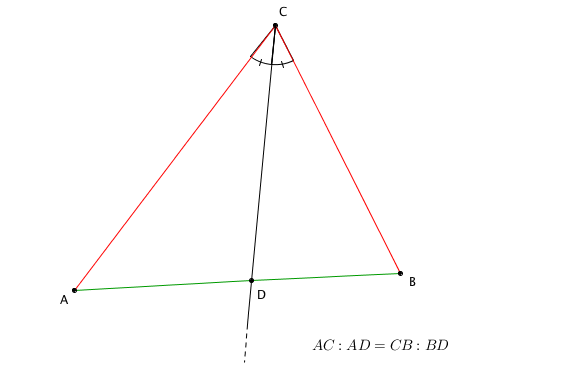
TEOREMA: La bisettrice di un angolo interno di un triangolo divide il lato opposto in parti proporzionali agli altri due.