In questa lezione daremo le principali definizioni dei vari tipi di angolo e ne studieremo le proprietà da un punto di vista molto astratto. Lasceremo infatti a questa lezione il compito di associare a ogni angolo una grandezza numerica che ne misuri l’ampiezza (definendo quindi il concetto di radiante e di grado).
Definizione
Consideriamo due semirette nel piano, che condividono la stessa origine. Prese insieme, queste due semirette dividono il piano in due parti. Oguna di queste due parti (semirette comprese) è chiamata angolo.
Inoltre:
- Le semirette si dicono lati dell’angolo;
- L’origine delle semirette si dice vertice dell’angolo.
I punti di un angolo che non appartengono ai lati costituiscono l’interno dell’angolo, mentre tutti gli altri punti (sempre esclusi quelli dei lati) si dicono esterni.

Notazione: di solito un angolo si indica con una lettera greca ($\alpha, \beta, \gamma \ldots$), una semiretta con una lettera minuscola dell’alfabeto latino ($a, b, c \ldots$) e un vertice con una lettera maiuscola dell’alfabeto latino ($O, A, B \ldots$).
Come abbiamo visto ogni volta che prendiamo in considerazione due semirette che hanno la stessa origine, stiamo di fatto osservando due angoli. Intuitivamente, possiamo dire che in generale questi angoli hanno ampiezze differenti, ma per il momento non abbiamo ancora definito cosa sia l’ampiezza (lo facciamo in questa lezione). Aggiriamo dunque il problema in questo modo:
Definizione
Un angolo è concavo se contiene al suo interno il prolungamento dei suoi lati, mentre un angolo sarà convesso se ciò non avviene.
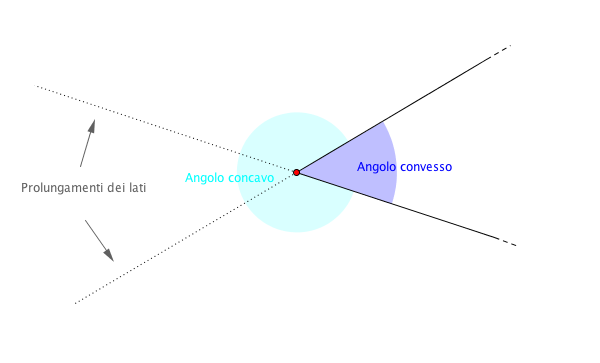
Quindi, in generale, i due angoli determinati da due semirette aventi la stessa origine sono uno concavo e l’altro convesso. L’unica circostanza in cui questo non accade è quando le due semirette sono una il prolungamento dell’altra: in questo caso ciascuno dei due angoli viene chiamato angolo piatto, che è un angolo convesso.
Altri angoli interessanti sono dati dal “caso limite” in cui i lati sono sovrapposti. L’angolo concavo così determinato viene detto angolo giro, mentre l’altro si chiama angolo nullo (così chiamato perchè privo di interno).

Definizione
Diciamo che un angolo $\alpha$ è minore di un angolo $\beta$ ($\alpha < \beta$) se $\alpha$ può essere interamente contenuto all’interno di $\beta$. Invece, diciamo che $\alpha$ è maggiore di $\beta$ ($\alpha > \beta$) quando questo non è possibile.
Definizione
Si chiama bisettrice di un angolo la semiretta che ha come origine il vertice dell’angolo, che divide l’angolo in due parti congruenti.

È possibile dimostrare che la bisettrice di un angolo è unica: motivo per cui diciamo “la bisettrice” e non “una bisettrice”.
Se consideriamo un angolo piatto e ne costruiamo la bisettrice, ciascuno degli angoli congruenti che si vengono a formare viene chiamato angolo retto. L’importanza di questo angolo è tale da renderlo uno “spartiacque” all’interno della caratterizzazione degli angoli:
Definizione
Un angolo minore di un angolo retto viene detto acuto, mentre un angolo maggiore di un angolo retto ma minore o uguale di un angolo piatto viene detto ottuso.

Definizione
Due angoli $\alpha$ e $\beta$ di un piano si dicono consecutivi se hanno lo stesso vertice e hanno in comune solamente i punti di un lato.
I lati che $\alpha$ e $\beta$ non hanno in comune formano, a loro volta, due angoli. Di questi due angoli, quello che contiene il lato comune a $\alpha$ e $\beta$ si dice somma di $\alpha$ e $\beta$.
Due angoli consecutivi si dicono adiacenti se i lati che non hanno in comune sono uno sul prolungamento dell’altro.
![]()
Dati due angoli $\alpha$ e $\beta$, diremo che:
- $\alpha$ e $\beta$ sono complementari se $\alpha + \beta$ è un angolo retto;
- $\alpha$ e $\beta$ sono supplementari se $\alpha + \beta$ è un angolo piatto;
- $\alpha$ e $\beta$ sono esplementari se $\alpha + \beta$ è un angolo giro.
Notiamo che due angoli adiacenti sono sempre supplementari.
Definizione
Due angoli convessi si dicono opposti al vertice se ciascun lato dell’uno è il prolungamento di un lato dell’altro.
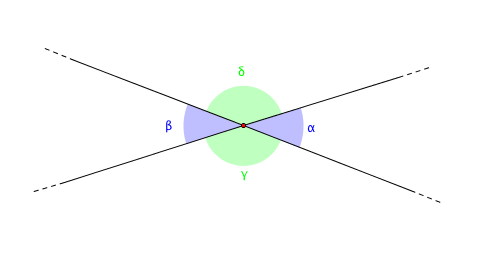
Concludiamo con un risultato di fondamentale importanza nella risoluzione di molti problemi di geometria euclidea:
TEOREMA: Due angoli opposti al vertice sono congruenti.
Dimostrazione. Consideriamo gli angoli $\alpha$ e $\beta$ nella precedente figura. Entrambi sono supplementari dello stesso angolo $\gamma$, dato che i lati di un angolo sono i prolungamenti dei lati dell’altro. Di conseguenza non può che essere $\alpha \cong \beta$.
La dimostrazione del fatto che $\gamma \cong \delta$ è del tutto analoga.
Revisione scientifica a cura di Marco Guglielmino